算法设计课程复习

分治法

计算阶乘n!

设计递归函数，计算n!的值，其中n>0。

int factorial(int n){
    if(n==1) return 1;
    else return factorial(n-1)*n;
}

Fibonacci数列

$$F_n=F_{n-1}+F_{n-2},F_1=F_2=1$$

Hanoi塔

假定n-1个盘子的转移算法已确定，对n个圆盘的问题：

​ 第1步：把A上面的n-1个圆盘经C转移到B上

​ 第2步：把A最下面的一个圆盘移到C上

​ 第3步：把B上的n-1圆盘经A转移到C上

转移完毕。

算法分析：令h(n)表示n个圆盘所需要的转移盘次，则算法复杂度为？

$$h(n) = 2h(n-1) + 1, h(1)=1$$ $$h(n) = 2^n -1$$

分治算法总体思想

1. 将求解的较大规模的问题分割成k个更小规模的子问题。对这k个子问题分别求解。

   比如上面的factorial函数，将n规模的任务缩小为n-1规模的任务。任务规模不一定缩小为n-1，也可能是n/2（如：折半查找）等等。

2. 如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

3. 将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

   

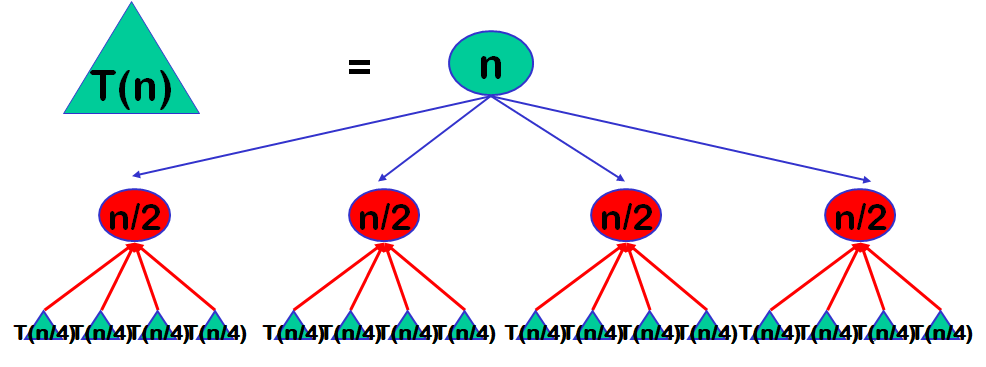
分治法的设计思想

​ 将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。凡治众如治寡，分数是也。—-孙子兵法

分治法的适用条件

分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定的程度就可以容易地解决；
• 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
• 利用该问题分解出的子问题的解可以合并为该问题的解；
• 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

这条特征涉及到分治法的效率，如果各子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。

分治法的基本步骤(重要)

divide-and-conquer(P)
{
    if ( | P | <= n0) adhoc(P); //解决小规模的问题
    divide P into smaller subinstances P1,P2,…,Pk；//分解问题
    for (i=1,i<=k,i++)
        yi=divide-and-conquer(Pi); //递归的解各子问题
    return merge(y1,…,yk); //将各子问题的解合并为原问题的解
}

分治法的复杂性分析(重要)

一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：

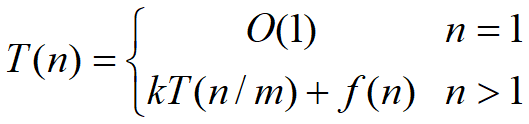
通过迭代法求得方程的解（记住$n^{\log_{m}k}$，以后分析算法复杂度的时候会用到）：

二分查找

给定已按升序排好序的n个元素，现要在这n个元素中找出一特定元素。

递归写法：

int BinarySearch (int x, int a[], intlow int high ){
    //递归实现二分查找算法，找不到返回-1
    if ( low > high) return -1;
    mid = (low+high)/2;
    
    if(x==a[mid]) return mid;
    if (x>a[mid]) return BinarySearch(x, a, mid+1, high);
    else return BinarySearch(x, a, low, mid-1);
}

非递归写法：

int Search_Bin ( SSTable ST, KeyType kval ) {
    low = 1; high = ST.length; // 置区间初值
    while (low <= high) {
        mid = (low + high) / 2;
        if ( kval == ST.elem[mid].key )
            return mid; // 找到待查元素
        else if ( kval < ST.elem[mid].key) )
            high = mid - 1; // 继续在前半区间进行查找
        else low = mid + 1; // 继续在后半区间进行查找
    }
    return -1;
}

快速排序

快速排序是对气泡排序的一种改进方法。它是由C.A.R. Hoare于1962年提出的。

基本思想是任取待排序对象序列中的某个对象 (例如取第一个对象) 作为基准, 按照该对象的排序码大小,将整个对象序列划分为左右两个子序列：左序列 ≤ 基准对象 ≤ 右序列

在快速排序中，记录的比较和交换是从两端向中间进行的，关键字较大的记录一次就能交换到后面单元，关键字较小的记录一次就能交换到前面单元，记录每次移动的距离较大，因而总的比较和移动次数较少。

private static void qSort(int p, int r)
{
    if (p<r) {
        int q=partition(p,r); //划分
        qSort (p,q-1); //对左半段排序
        qSort (q+1,r); //对右半段排序
    }
}

private static int partition (int p, int r)
{
    int i = p,
    j = r + 1;
    Comparable x = a[p];
    // 将>= x的元素交换到左边区域
    // 将<= x的元素交换到右边区域
    while (true) {
        while (a[++i].compareTo(x) < 0);
        while (a[—j].compareTo(x) > 0);
        if (i >= j) break;
        MyMath.swap(a, i, j);
    }
    a[p] = a[j];
    a[j] = x;
    return j;
}

​ 快速排序算法的性能取决于划分的对称性。通过修改算法partition，可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每一步中，当数组还没有被划分时，可以在a[p:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的，从而可以期望划分是较对称的。

private static int randomizedPartition (int p, int r)
{
int i = random(p,r);
MyMath.swap(a, i, p);
return partition (p, r);
}

最坏时间复杂度：O(n^2)
平均时间复杂度：O(nlogn)
辅助空间：O(n)或O(logn)
稳定性：不稳定

合并排序

算法mergeSort的过程。

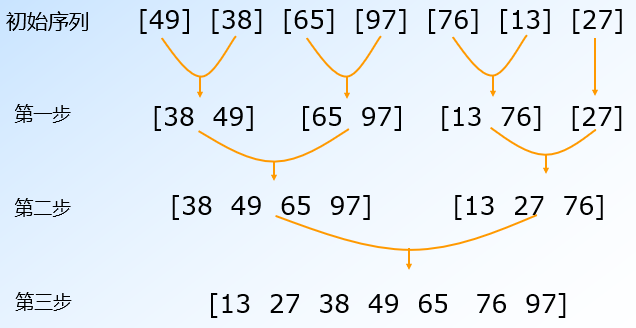
基本思想：将待排序元素分成大小大致相同的2个子集合，分别对2个子集合进行排序，最终将排好序的子集合合并成为所要求的排好序的集合。

public static void mergeSort(Comparable a[], int left, int right)
{
    if (left<right) {//至少有2个元素
        int i=(left+right)/2; //取中点
        mergeSort(a, left, i);
        mergeSort(a, i+1, right);
        merge(a, b, left, i, right); //合并到数组b
        copy(a, b, left, right); //复制回数组a
    }
}

复杂度分析：

$$T(n) = \left \{ \begin{matrix} O(1) & n<=1\\ 2T(n/2)+O(n) & n>1\end{matrix} \right.$$

T(n)=O(logn)渐进意义下的最优算法。

最坏时间复杂度：O(nlogn)
平均时间复杂度：O(nlogn)
辅助空间：O(n)
稳定性：稳定

大整数的乘法

请设计一个有效的算法，可以进行两个n位大整数的乘法运算。

tip：算法分析，更多追求的是算法设计思想，别太深究代码中的错误。你如果硬要深究，我就说这是伪代码，哼(￢︿̫̿￢☆)

$$X = a 2^{n/2}+b$$ $$Y = c 2^{n/2}+d$$ $$XY = ac 2^n + (ad+bc) 2^{n/2} + bd$$

$$XY = ac2^n + ((a-b)(d-c)+ac+bd)2^{n/2}+bd$$

或

$$XY = ac 2^n + ((a+c)(b+d)-ac-bd) 2^{n/2} + bd$$

细节问题：两个XY的复杂度都是O(nlog3)，但考虑到a+c,b+d可能得到m+1位的结果，使问题的规模变大，故不选择第2种方案。

更快的方法??

如果将大整数分成更多段，用更复杂的方式把它们组合起来，将有可能得到更优的算法。

最终的，这个思想导致了快速傅利叶变换(Fast Fourier Transform)的产生。该方法也可以看作是一个复杂的分治算法，对于大整数乘法，它能在O(nlogn)时间内解决。

是否能找到线性时间的算法？

目前为止还没有结果。

Strassen矩阵乘法

传统方法：$O(n^3)$
分治法: 使用与上例类似的技术，将矩阵A，B和C中每一矩阵都分块成4个大小相等的子矩阵。由此可将方程C=AB重写为：

$$\begin{bmatrix}C_{11} &C_{12} \\\\ C_{21} & C_{22} \end{bmatrix} = \begin{bmatrix}A_{11} &A_{12} \\\\ A_{21} & A_{22} \end{bmatrix}\begin{bmatrix}B_{11} &B_{12} \\\\ B_{21} & B_{22} \end{bmatrix}$$

由此可得：

$$C_{11}= A_{11}B_{11}+A_{12}B_{21}\\\\C_{12}=A_{11}B_{12}+A_{12}B_{22}\\\\C_{21}=A_{21}B_{11}+A_{22}B_{21}\\\\C_{22}=A_{21}B_{12}+A_{22}B_{22}$$

为了降低时间复杂度，必须减少乘法的次数。

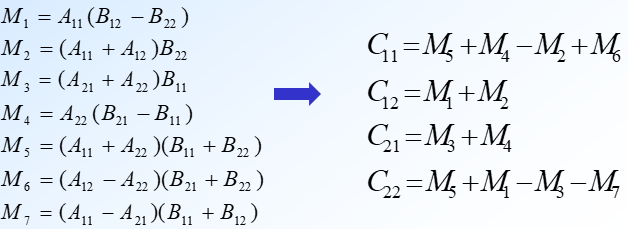
更快的方法??

Hopcroft和Kerr已经证明(1971)，计算2个２×２矩阵的乘积，7次乘法是必要的。因此，要想进一步改进矩阵乘法的时间复杂性，就不能再基于计算2×2矩阵的7次乘法的方法了。

或许应当研究３×３或５×５矩阵的更好算法。
在Strassen之后又有许多算法改进了矩阵乘法的计算时间复杂性。目前最好的计算时间上界是 $O(n^{2.376})$

是否能找到$O(n^2)$的算法？

目前为止还没有结果。

思考题

给定a，设计出求$a^n$的算法。

设计算法，找出数组a[n]的中位数。

设计算法，找出数组a[n]中序为k的数。

设计算法，输出数组a[n]中所有序为奇数的数。

设计算法，计算序列a[n]中的逆序数。

假设a[0:m]，a[m:n]均升序，设计算法，计算序列a[n]中的逆序数。

查找数组a[n]中的最大元素，至少需要多少次比较?

查找数组a[n]中的最大和最小元素，用最少的元素比较次数。

查找数组a[n]中的第k小的元素（k相对于n比较小)；

查找数组a[n]中的中位数（序号为n/2)；

查找数组a[n]中的最大元素，至少需要多少次比较?

查找数组a[n]中的最大和最小元素，用最少的元素比较次数。

查找数组a[n]中的第k小的元素（k相对于n比较小)；

查找数组a[n]中的中位数（序号为n/2)；

给定有序表A[1:n]，修改合并排序算法，求出该有序表的逆序对数。

参考

汕头大学算法分析设计课程PPT__老师（CHYD）

补充

人们从大量实践中发现，在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。